Jörg Hennig: Home, Research, Publications, Teaching, CV
My primary research interests lie in the field of General Relativity — Albert Einstein’s theory of gravitation.
In particular, I am studying
- axisymmetric and stationary spacetimes,
- cosmological models,
- the application of pseudo-spectral methods to the numerical solution of hyperbolic PDEs.
Axisymmetric and stationary spacetimes can be used as a mathematical description of equilibrium configurations in General Relativity. For example, this could be a configuration with a central black hole and surrounding matter. It is possible to show that some statements for the Kerr solution (the explicitly known solution describing a single rotating black hole in vacuum) are still valid if the black hole is disturbed by surrounding matter. In particular, my collaborators and I proved a universal inequality for such black holes, which shows the existence of an upper bound for the rotation rate. Moreover, using methods from soliton theory, it is possible to show that the central black hole always has a so-called inner Cauchy horizon.
Furthermore, I study axisymmetric two-black-hole configurations, and it was possible to show that these configurations cannot be in equilibrium. This has provided a negative answer to the long-discussed balance problem for two black holes. In the case with charged black holes or with more then two black holes, the problem is still open, though some progress has been made regarding the form of possible solutions.
Two aligned black holes
cannot be in equilibrium.
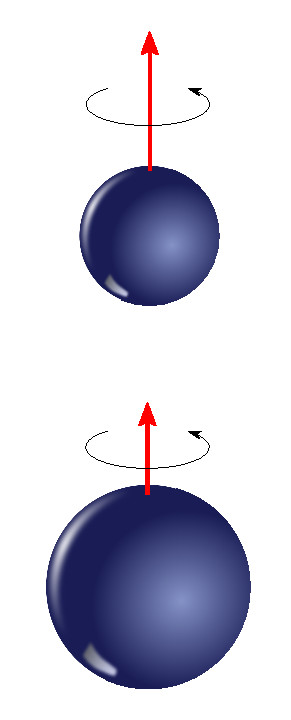
Illustration of the causal structure of a particular exact Gowdy-symmetric cosmological model. Details can be found here.
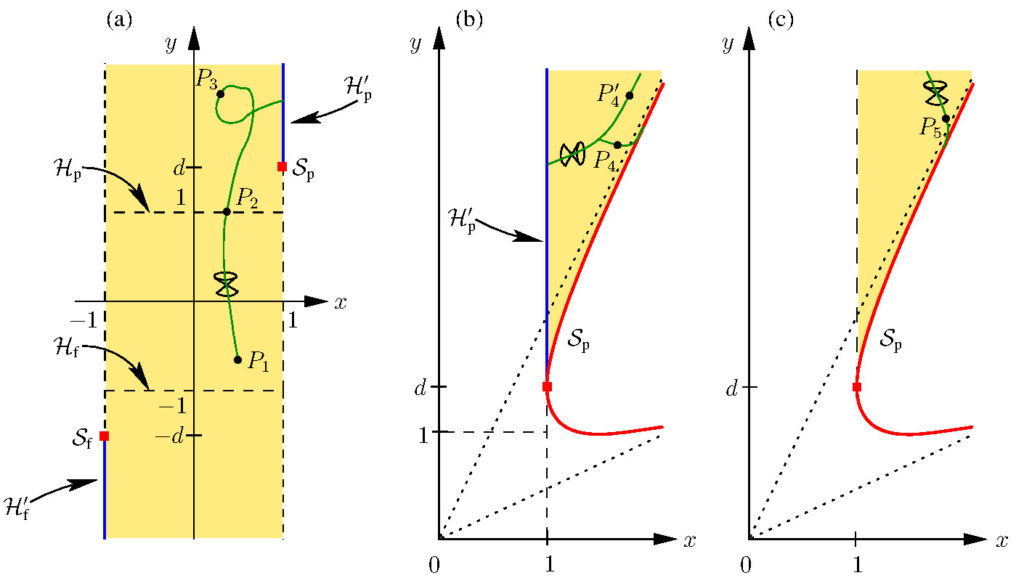
Similar mathematical techniques from soliton theory can also be applied to an investigation of Gowdy-symmetric spacetimes, which are cosmological models with two symmetries. I am particularly interested in local and global existence of solutions with different spatial topologies, the study of in properties of these solutions and the derivation of exact solutions.
Remarkably, one can construct cosmological models that have closed causal curves, i.e. solutions where a genuine time travel would be possible — in clear violation of causality.
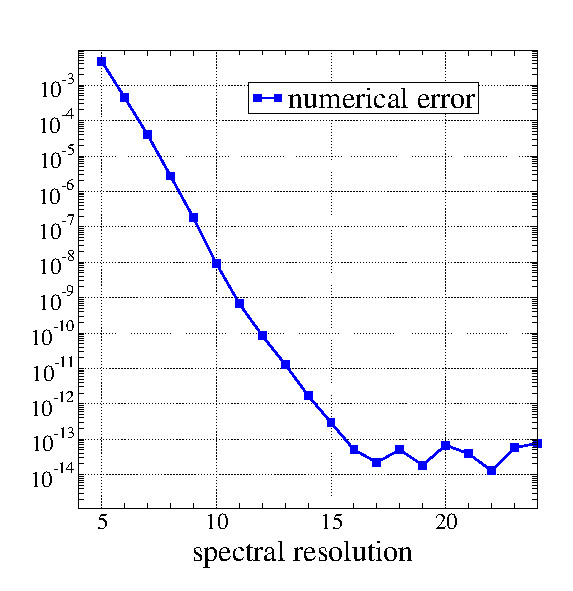
I am also interested in numerical relativity, where the complicated differential equations following from Einstein’s field equations are solved with numerical methods. This is important for the simulation of dynamical processes within the theory of General Relativity. As a promising new approach, my collaborator and I have developed a fully pseudo-spectral numerical scheme, in which spectral expansions with respect to space and time are used. In the case of sufficiently smooth solutions, this guarantees highly accurate numerical solutions with an accuracy close to machine accuracy for a moderate number of grid points.
Convergence plot for a sample problem.